Er is een bijna religieuze discussie gaande op het internet of je nu wel of geen nachtverlaging moet toepassen bij een (hybride) warmtepomp. Ik heb hier een bierviltberekening op los gelaten.
Warmtecapaciteit
Hier begint het in mijn ogen mee. De binnenkant van de woning heeft een bepaalde warmtecapaciteit. Al het beton, hout, behang, gipsplaat, isolatie, meubels, etc heeft een bepaalde massa en een bepaalde capaciteit wat betreft warmte. En om die hele inhoud 1 graad op te warmen is een bepaalde hoeveelheid energie nodig waarbij het omgekeerde ook geldt. Dus om het huis 1 graad af te koelen moet er een bepaalde hoeveelheid aan energie ontsnappen uit het huis.
Ik heb een poging gewaagd om voor mijn woning een warmtecapaciteit te berekenen. Als ik alleen het beton neem kom ik uit op een idioot getal van 68m3 beton voor onze woning. 1m3 beton is omgerekend 2400 kilo en 1 kilo beton kost 0,84kJ om 1 graad op te warmen. Omgerekend dus 137MJ is er nodig om al het beton 1 graad op te warmen.
Hierover later meer.
Warmteverlies
Daarnaast verliest een woning een bepaalde hoeveelheid energie per seconde. Dit is te berekenen door middel van een warmteverliesberekening. Ik heb een warmteverliesberekening gemaakt van mijn eigen woning. Bij -10 verliest mijn woning ruim 4.3kW, bij 0 is dit 3.4kW en bij +10 nog 2.6kW.
Aangezien 1W gelijk staat aan 1 Joule per seconde. is ook om te rekenen hoeveel warmte er per uur verloren gaat. Bijvoorbeeld voor 0 graden is dit 3400J/s * 3600s = 12.24MJ.
Dan is dus ook uit te rekenen hoeveel een woning in een uur afkoelt als de verwarming uit staat, immers is de warmtecapaciteit ook bekend.
Rekenvoorbeeld en disclaimer
In onderstaand voorbeeld heb ik een forse correctiefactor moeten toepassen op de warmtecapaciteit van mijn woning. Als mijn woning 137MJ moet verliezen om 1 graad af te koelen duurt het bij 0 graden 137/12,24 = dik 11 uur voordat mijn woning 1 graad is afgekoeld. En zo werkt het niet in de praktijk. Met 0 graden buiten duurt het een uur of 2 a 3 voordat mijn woning 1 graad is afgekoeld.
Ik ga in onderstaand voorbeeld uit van een correctiefactor van 0.3 waarmee onze warmtecapaciteit per graad uit komt op 41MJ.
Daarnaast ga ik uit van een warmtepomp met een maximale capaciteit van 5kW.
Klokprogramma
In dit voorbeeld ga ik uit van het volgende klokprogramma:
- 00:00 – 09:00 = 18.0 graden
- 09:00 – 00:00 = 20.0 graden
Tabel
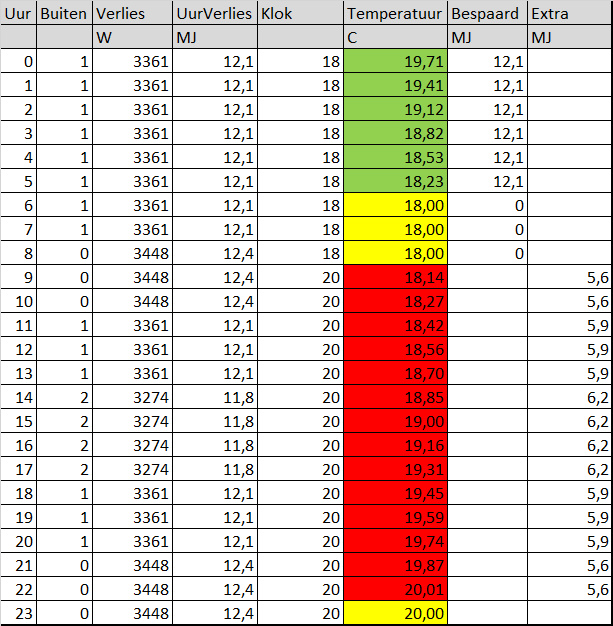
Ik ga hier uit van een gemiddelde winterdag zoals nu. Overdag een graad of 2 in de nacht rond het vriespunt. In de kolom staat het warmteverlies gedurende dat uur, afhankelijk van de buitentemperatuur.
- Uurverlies: Dit is het verlies in MJ wat de warmtepomp dus moet compenseren om de woning op temperatuur te houden.
- Klok: Het klokprogramma van de thermostaat
- Temperatuur: Dit is de temperatuur in de woonkamer waar de thermostaat hangt.
- Bespaard: Dit is de uitgespaarde energie omdat de warmtepomp niet hoeft te draaien vanwege de nachtverlaging
- Extra: Dit is wat de warmtepomp extra per uur aan MJ kan leveren om de woonkamer weer op te warmen.
Wat voorbeelden per uur om dit verder uit te leggen.
00:00 – 01:00
Dit is het eerste uur dat de nachtverlaging is in gegaan. Hier kan dus worden bespaard. De warmtepomp zou hier 12,1MJ in dat hele uur voor nodig hebben gehad om het warmteverlies te compenseren. Maar de warmtepomp staat uit en dus koelt de woning af. De woning verliest 12,1MJ aan energie wat gelijk staat aan 12,1 / 41 = 0,3 graden.
06:00 – 07:00
Hier raakt de woning de ingestelde temperatuur op de klokthermostaat en gaat de warmtepomp weer aan de slag om de woning niet verder te laten afkoelen.
09:00 – 10:00
Hier moet de warmtepomp aan de bak! De klokthermostaat gaat 2 graden omhoog en het verlies in warmte moet nu gecompenseerd worden. De warmtepomp heeft een maximale capaciteit van 5kW terwijl er al 3448W nodig is om de woning niet nog verder af te laten koelen. De capaciteit die over is is 5000 – 3448 = 1552W. In een uur is dat 1552 * 3600 = 5.6MJ. Die 5.6MJ extra zorgt ervoor dat de woning van 18.0 naar 18,14 graden op kan warmen.
Het probleem
Die 6 uur nachtverlaging zorgt ervoor dat de warmtepomp 14 uur op vol vermogen moet draaien om het warmteverlies te compenseren. En in dit geval komt de woning nog op temperatuur. Met een iets kleinere warmtepomp, of een grotere nachtverlaging, komt de woning niet meer op temperatuur en koelt dag na dag de woning steeds verder af.
Stille modus
Daar had ik in mijn voorbeeld nog niet eens rekening mee gehouden. Stel dat tussen 23:00 en 08:00 de stille modus aan staat waardoor de warmtepomp geen 5kW warmte kan leveren maar slechts 2.5kW.Dan koelt de woning dus nog verder af en krijgt de warmtepomp het nog zwaarder om de woning weer op temperatuur te krijgen.
Defrosts
Update, bedankt Wouter! En rond het vriespunt gaat er nog wat anders mee spelen, de defrosts! Doordat de warmtepomp langer op vol vermogen moet draaien is de kans op defrosts ook een stuk groter. En door defrosts gaat het effectieve vermogen van de warmtepomp ook nog eens onderuit.
Dus op vol vermogen moeten draaien om de verloren warmte te compenseren heeft nog meer hobbels!
Nachtverlaging?
Die zal iedereen met een hybride warmtepomp voor zichzelf moeten beantwoorden. Wil je zo lang als mogelijk op de warmtepomp draaien, door bijvoorbeeld overschot aan zonnestroom, dan zou ik GEEN nachtverlaging toepassen maar dan moet de stille modus ook uit.
Ik denk genoeg voer voor discussie.

Dankjewel, heel inzichtelijke en relevante berekening voor deze tijd van het jaar.
Vooral dat benodigd vermogen voor compensatie van warmteverlies in de nacht, nauwelijk overcapaciteit overlaat om voor extra opwarming te zorgen. Zeker niet wanneer, zoals nu, ook de-frostcycli worden doorlopen en dus het beschikbare vermogen afneemt.
Ha Martin,
Interessante gedachtegang. Ik zie echter een aantal aanvullende zaken als input op deze discussie:
1) bij een volstrekt lineair verband en er vanuitgaande dat je alle warmteverliezen 1:1 wil compenseren met je warmtepomp, is een lagere dT ook van invloed op je COP en dus elektriciteitsverbruik. Dit is wellicht theoretisch van aard met deze temperaturen maar toch en pleit dus tegen nachtverlaging.
2) voor nachtverlaging: je gaat er vanuit dat het vermogen waarmee je warmte verliest 100% in moet vullen met warmte uit de WP. Als er aanvullende warmte is, zal die de woning als ‘verlies’ verlaten ipv dat die aanvullende warmte een beetje warmte van van de warmtepomp verdringt. Met name de zon doet zelfs in deze dagen wel wat.
Reken oefening: zonnepaneel heeft een rendement van 20% bij 1 kW/m2 en T = 20C. Een paneel van 1,6 m2 dat 50 W elektrisch produceert, produceert dus 50/1,6 = 31 W/m2. En om dat te maken, valt er dus 31 / 0,2 = 156 W/m2 zonlicht op. Das best veel als je bedenkt hoeveel m2 huis zonlicht ontvangt en reduceert dus het vermogen waarmee je warmte verliest, zeker als dat vermogen door je ramen intreedt.
Wellicht interessant om eens in je excel toe te voegen?
Overigens is hier het argument iets rechtlijniger: warme voeten bij een ruimte temperatuur van 18 graden is acceptabel. Koude vloer bij 20 graden ruimte temperatuur niet. Dus ik zet m op nachtverlaging, stook twintig minuten in de ochtend en dan gaan we werken/ naar school en dus de temperatuur weer terug naar 18. Scheelt veel MJ aan verlies!
Een mooie en simpele rekensom. Dank.
Als je dan nog toevoegt, dat de COP ‘s-nachts lager is dan overdag (gezien de buitentemperatuur) en afkoeling ook niet lineair is. Bovendien mogelijk de warmtepomp op een hogere temperatuur moet stoken, dus minder efficiënt, wordt de rekensom heel wat ingewikkelder.
Overigens heeft Vincent wel een punt, denk alleen (zonder te rekenen), dat de nachtverlaging niet zo extreem moet zijn, maar slechts 1,5 graad. Dan kan je waarschijnlijk prima verwarmen. Hoeft Vincent in de ochtend maar een halve graad te stoken voor net aan voldoende comfort.
Het verschil in COP is met maar 1 graad verschil buiten niet heel groot. We hebben nu echt komkommerwinter waarbij dagtemperatuur nauwelijks hoger ligt dan in de nacht. Dat was ook het mooie aan het live voorbeeld van afgelopen weekend.
nederland kiest te klein das lekker goedkoop, ik koos veel te groot. een energion 9t. nachtverlagen doe ik met 2c, smorgens is het in 20 minuten zo weer 3 graden warmer, en zo kwam ik wel heel makkelijk van die ketel en gasaansluiting af. van het vastrecht gas kan ik bijna heel december het huis comfortabel warm houden. het is erg simpel, als je te klein kiest, kom je nooit van je ketel af, en je auto is waarschijnlijk te groot, maar daar zit je niet de hele dag in he.
anyways, ik verwarm voor 0,4kwh het huis snel weer warm, maar lager dan -8c heb ik nog niet ervaren (dec2022) en anders zitten er nog 2 heaters in.