Bewust in een nieuw blogpost. Ik denk dat ik een manier heb gevonden om grofweg te bepalen bij welke temperatuur een hybride warmtepomp het niet meer alleen af kan door gebruik te maken van de bekende Koevlaas2 formule.
Disclaimer
Dit is een hele grove berekening gebaseerd op een sterk vereenvoudigde weergave van hoe dit natuurkundig in elkaar steekt! Voor een goede berekening is onder andere een transmissieverliesberekening nodig van de woning!
Benadering
De Koevlaas2 formule bepaald het maximale vermogen benodigd om het huis warm te houden op een ontwerptemperatuur, doorgaans -10. Die uitkomst is dus het benodigde vermogen bij -10. Meestal is de kamertemperatuur in een woning 20 graden, dus bij grofweg 20 graden buiten gemiddeld is het warmteverlies 0. ( Normaliter wordt er uit gegaan van 18 graden, bijvoorbeeld met graaddagen ).
Een aangezien het warmteverlies min of meer een lineair verband heeft met de buitentemperatuur kom je op ( voorbeeld met 1500m3 gasverbruik):
- 1500*8/1650=7300W warmteverlies bij -10
- Warmteverlies bij 20 graden = 0.
- Afgeleide per graad is 7300 / 30 = 242W warmteverlies per graad
De ACE 4 heeft ruwweg 4000W verwarmingsvermogen dus bij 20 – ( 4000 / 242 ) = +4 graden houdt het ongeveer op. Bij de ACE 6 is dit ( 20 – 6000 / 242 ) = -5 graden.
Hier zitten allerlei mitsen en maren aan. Afgiftesysteem in huis moet goed zijn, er wordt geen rekening gehouden met houtkachels, verliezen door tocht, regen, wind op de gevel etc of de echte warmtecurve die een ACE4 of ACE6 kan leveren. Maar als uitgangspunt voor het instellen van parameter HP051 kan dit een hele zinvolle basis zijn.
Hier de waarden voor verschillende verbruiken:
| Gas | W | Per Graad | ACE4 | ACE6 |
| 800 | 3879 | 129 | -10 | -10 |
| 900 | 4364 | 145 | -8 | -10 |
| 1000 | 4848 | 162 | -5 | -10 |
| 1200 | 5818 | 194 | -1 | -10 |
| 1400 | 6788 | 226 | 2 | -7 |
| 1600 | 7758 | 259 | 5 | -3 |
| 1800 | 8727 | 291 | 6 | -1 |
| 2000 | 9697 | 323 | 8 | 1 |
| 2200 | 10667 | 356 | 9 | 3 |
| 2500 | 12121 | 404 | 10 | 5 |
| 3000 | 14545 | 485 | 12 | 8 |
| 7000 | 33939 | 1131 | 16 | 15 |
Disclaimer: Bij waarden onder nul gaat deze berekening dus deels mank omdat de warmtepomp bij lagere temperaturen minder warmte dan die 4000 of 6000W kan leveren, zeker als de buitenunit ook nog eens met enige regelmaat moet ontdooien!
Ik heb hier als voorbeeld ook weer de man met 2 woningen met in totaal 7000m3 gasverbruik genoemd. Een ACE 6 houdt dus al ruim boven de 15 graden er mee op omdat deze niet voldoende warmte kan leveren.
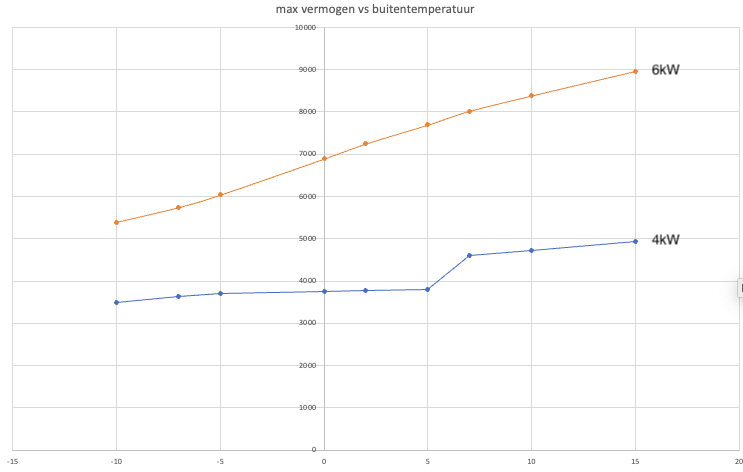
Dit zijn de grafieken van de ACE4 en ACE6 wat betreft de buitenunit zou kunnen leveren. ( Met dank aan onbekende auteur voor deze grafiek ).

Om het praktische warmteverlies per ruimte te bepalen kan je dit doen door in een ruimte met een elektrische verwarming het energieverbruik te meten bij x buitentemperatuur. In combinatie met een andere meting van het gasverbruik per uur kan je ook het systeemrendement uitrekenen. Bij mij bleek 1 m3 gas, effectief 5kW warmte te leveren in de ruimte. Het lineaire effect van warmteverlies tov de buitentemperatuur in combinatie met het systeemrendement bepaald in hoeverre de warmtepomp kan voldoen aan de warmtebehoefte. Klinkt misschien ingewikkeld maar het geeft wel een realistisch beeld wat je van de warmtepomp kan verwachten bij x buitentemperatuur.
19560216 -149
19420126 -145
19420127 -145
19290214 -141
19420121 -140
19560201 -140
19420122 -136
19290211 -135
19381219 -134
19381220 -134
19870114 -132
19290212 -129
19420120 -128
19970102 -126
19081229 -125
19790105 -124
19560223 -122
19560217 -121
20120204 -121
19081230 -120
19400122 -120
19400213 -119
19290215 -118
19850107 -118
19070123 -116
19781231 -116
19560224 -115
19120203 -114
19970101 -114
19870111 -113
19400119 -112
19560202 -112
19630110 -112
19630117 -112
19170203 -111
19461221 -111
19790101 -111
19790106 -110
19251205 -107
19290213 -107
19461220 -107
19870112 -107
19420203 -106
19081231 -105
19381218 -105
19420207 -105
19420222 -105
19630118 -105
19120204 -104
19290216 -103
19381222 -103
19420119 -103
19470107 -103
19540201 -103
19680113 -103
19081228 -102
19790102 -102
19271220 -101
19381223 -101
19470129 -101
19690214 -101
19850115 -101
19010106 -100
19220124 -100
dit zijn alle daggemiddelden waarbij het dus 24h -10 gemiddeld was. in totaal 64 dagen in 140 jaar tijd. Waar doen we moeilijk over. Als je echt bang bent koop je een laserkachel erbij
-10 wordt nog wel steeds als ontwerptemperatuur genomen. Overigens veranderd het verhaal niet met dat een hybride warmtepomp ergens een omslagmoment heeft. En met deze blogpost probeer ik een ruwe inschatting te maken waar dat omslagpunt ongeveer zit afhankelijk van het gasverbruik.
Hi Martin, ik ben groot voorstander van de natuurkundige benadering. Cijfers zijn cijfers en de rest is emotie. Je laatste grafiek geeft ook mooi aan waarom de Elga standaard wordt begrensd op 4° en suggereert zelfs dat die begrenzing eerder op 6-7° zou mogen liggen. Echter, Luuk Oosterbaan stelt ook op natuurkundige gronden dat ver onder die grens de Elga nog (goedkope!) Joules toevoegt aan je verwarmingssysteem zolang de COP boven pak ‘m beet 2,7 ligt. En dat punt ligt ergens rond de -7° volgens de specs. Dit alles uitgaande van een hybride opstelling natuurlijk. En daar zit ‘m de kneep zoals je zelf beschrijft. Een hybride vermomd als all-electric installeren is vragen om problemen natuurlijk, tenzij fors overbemeten.
Hoe denk jij over dat hybride draaien tot ver onder nul?
@Guus,
Hybride kan, in sommige situaties, prima mee draaien tot ver onder nul. Dat is precies waarom ik lans wil breken voor de ACE 6 ipv de ACE 4. Bij de ACE 4 houdt het spelletje/feest inderdaad al veel eerder op. Zeker op het moment waar de grafiek een dip laat zien.
Maar bij een laag energieverbruik kan de ACE hybride prima mee. Sterker; Ik draai er solo mee met een goede (S)COP